�@�@�@�@�@..�@!!�@�@�@�_(^��^)�^
���� �y�[�W �� ���� �Q�� �N�I���e�Byone12053.zouri.ne.jp
��1v3-0vv0 ��v�s�����恛����1-v-3
�����s�R���b�g���̂Ȃ݂�
�@������
�@�@�܂��@�R�@���@�݂Ђ炫�@�́@���������@���@���߂܂�
18 �ǁ@�~�@10 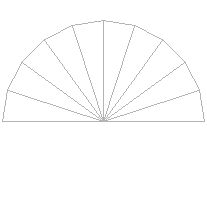 �͂イ YAMA |
�@�@ | 36 �ǁ@�~�@10 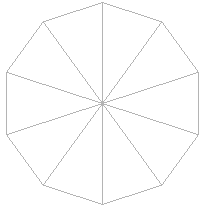 �������イ YODA |
�@�@�@�R�@�ځ@�݂��� �u���b�a�@�@�@�@�@���@�@�@�@�@�A�@���@�ځ@�Ƃ��� �X�N�����[
�@�@���Ɂ@���@���@�Ƃ����@�܂��Ɂ@�ق������@���@�Ƃ��Ă����܂�
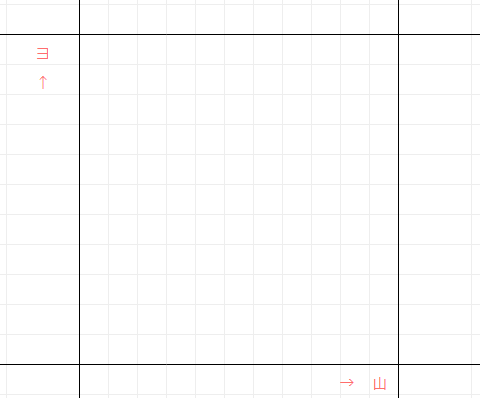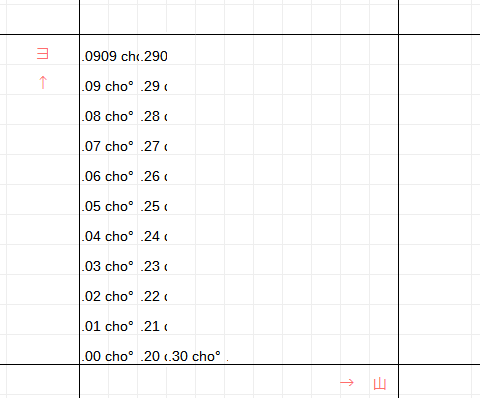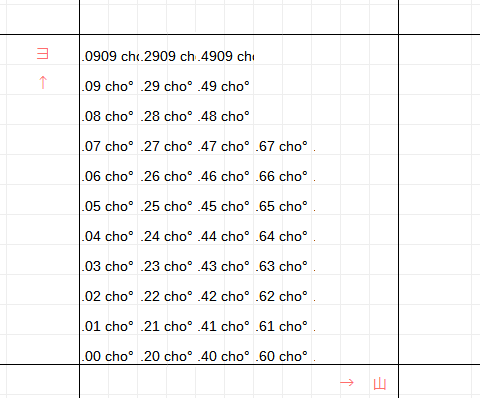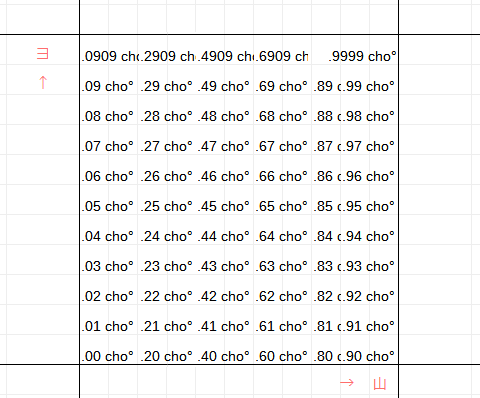
�����ɏЉ������܂��B�����ɏЉ������܂��B�����ɏЉ������܂��B�����ɏЉ������܂��B�����ɏЉ������܂��B�����ɏЉ������܂��B�����ɏЉ������܂��B�����ɏЉ������܂��B�����ɏЉ������܂��B�����ɏЉ������܂��B�����ɏЉ������܂��B�����ɏЉ������܂��B |
�@�����ς�
| �@ IF(ABS(MOD(�l,200))<=100 , ABS(MOD(�l,200)) , 200-ABS(MOD(�l,200))) �@ |
�@�@�܂��A�n�[�t�^�[���@���@�����Ă��邩�@���Ȃ����@���݂�
�@�@�@�����Ă���Ȃ�A200�@����@�Ђ��܂�
�@�@�@�@�����Ă��Ȃ��Ȃ�A200�@���@�Ђ��܂�
�@�@IF ( ABS ( MOD ( �l , 200 )) <= 100,
�@�@�@cho�� �l�@���@200�@�Ł@����� �Ƃ��@�́@���܂�@�́@�����������@��
| �@�� �@�� �@�� �@�� �@�� �@�� �@�� �@�� �@�� �@�� |
�@�@, ABS ( MOD ( �l , 200 )) , �@�@�����@100�@���� �Ȃ�@���� �������@�� �@�@, 200 - ABS ( MOD ( �l , 200 ))) �@�@�����@100�@���@���������Ȃ�@200�@����@���� �������@���@�Ђ��܂� |
�@��[�܁[�@�@�@�@�@�@�@�@�@�@�@�@�@��@��[���[
�X�e���W�A���@�ł����Ƃ���́@�� �� �p ���@���@�A�`�����O���[�h�@�� �����Ƃ���́@�R
��[�܁[�@�u���킵���v�@�Ł@�����N
�P�W �ǁ@ �P �� ��
�O.�P �Y�@�P �� ��
�����V�R�p�x
�ɂ��イ�Ԃ@��[�܁[�@�����ǁ@��������
�� �� �V �R �p �x �� �� �l�@�@�@�@�c�@�� �� �P�^
������@(�p�C)�@�Ɓ@������@(�f�V)�@�@�Ƃ��@���݂��킹�邱�Ƃ�
�������Ă��@�Ɂ@�������@�����@�������@�@�@�@�@�@(�@�̂��́@�� �� �P�^�@)
���@�悤�����܂�
�� �Y �l�@�@�@�u�@�ł��ς��@(��)�@�v�@�@ �c�@(�@�����Ƃ����@�u�f�V�v�@���@�f�W�^�������ɂ��@)
�@��������
�@o�P�W �@���@����� �݂����������Ɂ@�̂��ā@�u�@�ɂ��イ�Ԃ@(��)�@�v�@�Ɓ@��ނ��Ƃɂ��Ă݂܂�
�@�@�@���邢��
�@�@�@�������Ă��@�������@�ɂ́@�u�@�Ƃ��Ɂ@���@�Ȃ��@�v�@�Ƃ��Ă����܂�
������ �E �����@�T�C�g�@�����N
�@��[���[�@�@�@�@�@�@�@�@�@�@�@�@�@��@��[�܁[
�R�U�ǁ@ �@�P�ʉ�
�O.1 turn�@�P�ʉ��@�@�@�@ �c�@(�@���@0.1 ��]�@�@�@���@�f�W�^�������ɂ��@)
�\���V���p�x
���イ�Ԃ@��[���[�@�����ǁ@��������
�\ �� �V �� �p �x �� �� �l�@�@�@�@�c�@�� �� �P�^
������@(�^�[��)�@�Ɓ@������@(�f�V)�@�@�Ƃ��@���݂��킹�邱�Ƃ�
�������Ă��@�Ɂ@�������@�����@�������@�@�@�@�@�@(�@�̂��́@�� �� �P�^�@)
���@�悤�����܂�
�� turn �l�@�@�@�u�@�ł����[��@(��)�@�v�@�@ �c�@(�@�����Ƃ����@�u�f�V�v�@���@�f�W�^�������ɂ��@)
�@��������
�@o�R�U �@���@����� �݂����������Ɂ@�̂��ā@�u�@���イ�Ԃ@(��)�@�v�@�Ɓ@��ނ��Ƃɂ��Ă݂܂�
�@�@�@���邢��
�@�@�@�������Ă��@�������@�́@�u�@�Ƃ��Ɂ@���@�Ȃ��@�v�@�Ƃ��Ă����܂�
0.4
������ �E �����@�T�C�g�@�����N
�@�������イ���@( 200 �� ���Z�b�g )
���@�����イ�@�k���Ƃ��@���Ђ傤�@�A�j��
200�@���@�������@cho���@�l
�@�@200�@���@�������@cho�� �l�@�́@�����ς��@( �� ���Ȃ��ق����� �� ������ )�@�Ɂ@�Ȃ�܂�
�@�@200�@cho���@�{�@�ԁ@cho���@���@(�@�ԁ@cho���@�́@�����ς��@)
�@�@�ꂢ
�@�@200�@cho���@�{�@82�@cho���@���@�@282�@cho���@���@�@82�@cho���@�́@�����ς�
�@�@200�@cho���@�{�@55�@cho���@���@�@255�@cho���@���@�@55�@cho���@�́@�����ς�
�@�͂� ���イ���@( ���肩���� 100 �n�[�t�^�[�� )
���@�����イ�@�k���Ƃ��@���Ђ傤�@�A�j��
200�@����@�����Ђ����@cho�� �l�@���@�����ς��@( �� ���Ȃ��ق����� �� ������ )�@�Ɂ@�Ȃ�܂�
�@�@200�@cho���@�|�@�ԁ@cho���@���@(�@�ԁ@cho���@�́@�����ς��@)
�ꂢ
�@�@200�@cho���@�|�@82�@cho���@���@�@118�@cho���@���@�@82�@cho���@�́@�����ς�
�@�@200�@cho���@�|�@55�@cho���@���@�@145�@cho���@���@�@55�@cho���@�́@�����ς�
( ���݂������� )�@
�ЂႭ �� �P�^�@���A�@�������@�̂ǂ����̂����A�n�[�t�^�[���@�Ɂ@�Ȃ�܂��B
���Ƃ��A�@
125 cho���@,�@�@333 cho���@,�@�@580 cho���@,�@..�@
�� �ЂႭ�� ���炢�� ���イ�������A
125 cho���@,�@�@333 cho���@,�@�@580 cho���@,�@..�@�Ȃǁ@���@����Ɂ@�Ȃ�܂��B
�@125 cho���@�́@200�@cho���@����@�Ђ��ā@�@75�@cho���@�Ɓ@���Ȃ��ق������@�Ɂ@�Ȃ�܂�
�@333 cho���@�́@400�@cho���@����@�Ђ��ā@�@67�@cho���@�Ɓ@���Ȃ��ق������@�Ɂ@�Ȃ�܂�
�@580 cho���@�́@600�@cho���@����@�Ђ��ā@�@20�@cho���@�Ɓ@���Ȃ��ق������@�Ɂ@�Ȃ�܂�
�@�}�C�i�X�@�l�@�@�@(�@���Ȃ��@�������@)
���@�����イ�@�k���Ƃ��@���Ђ傤�@�A�j��
�v���X�}�C�i�X ���Ⴍ�@�́@�ǂ����@���@�����ς��@( �� ���Ȃ��ق����� �� ������ )�@�Ɂ@�Ȃ�܂�
�@�@�@ �@ �@�| �ԁ@cho���@���@(�@�ԁ@cho���@�́@�����ς��@)
�ꂢ
�@�@�@ �@ �@�|22�@cho���@���@22�@cho���@�́@�����ς�
�@�@�@ �@ �@�|95�@cho���@���@95�@cho���@�́@�����ς�
�@�����@�@�@(�@�����ς��@)
���@�����イ�@�k���Ƃ��@���Ђ傤�@�A�j��
�� �������イ���@�@�� �n�[�t�^�[���@�@�� �v���X�}�C�i�X �@���@�܂Ƃ߂��
�����
200�@cho���@���@�Ȃ��@..�@���Ȃ��@�ق������@�ɂȂ�܂�
�ꂢ�@
�@�@82�@cho���@�́@�����ς�
�@�@282�@cho���@�@�@�|118�@cho���@�@�@482�@cho��
�@�|282�@cho���@�@�@�@118�@cho���@�@�|482�@cho���@�@�@�|82�@cho���@..�@�Ȃ�
�� ���ǂ�
�@���ق�@�����������@(�@����݂� �ɂ́@99.9999 ..�@cho���@)
������ł́@���݂������ā@�P�O�O�@cho���@���@���������@���Ɓ@���Ă��@�Ɂ@�����܂����B
m(_ _)m
�������A
�P�O�O�@�����傤�@( �P�O�O �� �ӂ��� )�@�Ł@�n�[�t�^�[���@���@�����Ă��܂��̂�
����݂ȁ@�߂�ł́@���́@�킸���@�Ɂ@�Ă܂�
�X�X.�X�X�X�X..�@���@����݂@���ق�@�����������@�Ɂ@�Ȃ�܂��B
�P�O�O�@�́@�����@�́@�n�[�t�^�[���@���@�������@���Ƃ́@�[���@�Ɂ@�Ȃ�܂��B
m(_ _)m
�@�@�ق���
���́@�ق������@�́@������@�u�@�͂��@�v�@���@���݂��܂��B
�߂�@��@���傤���傤�@�ɂ���Ắ@
������@(�@���Ⴍ �E ���� �E ���Ȃ� �E �}�C�i�X�@�ق������@)�@�ȂǂƁ@������
�Ђ傤����@�����@�ق������@�Ƃ����邩���@����܂���B�@
���A
�Ђ傤����@����₷���@�ق������@�ł��邪�@�䂦��
���ꂪ�@�������@���Ă��Ȃ��Ƃ��@�́@
������������@�́@�����邪��@�́@�͂�����@�Ɓ@
��������@�́@���イ���@���@�Ђ悤�Ɂ@�Ȃ�܂��B
m(_ _)m
�@����������
�R�@�́@���������@�Ɓ@���@�́@���������@���@�P�P�^�@���炵�ā@���킹�܂��B
�R�@�́@���������@�P�^�@(�@�P�O�@�̂��炢�@����@�ЂƃP�^�Ƃ��@)�@��
���@�́@�������@�@�P�^�@(�@�@�P�@�̂��炢�@����@�ЂƃP�^�Ƃ��@)�@��
�������Ɂ@�킯�ā@���߂���܂��B
�P�P�^�@���炵����A�������Ă��@���@( ���Y , ��turn�@�́@������ )�@���@���Ɂ@���邱�ƂȂ��A
���̂܂܁@�������킹�܂��B
�ꂢ�P
| �R�@�W�P �� ���@�V�Q �� |
�� �� �� |
���@42.5�@cho�� |
| 42.5�@cho���@�� | �� �� �� |
�@
�ꂢ�Q
| �R�@23.4 �� ���@86.4 �� |
�� �� �� |
���@12.34�@cho�� |
| 12.34�@cho���@�� | �� �� �� |
�@
�ꂢ�R
| �R�@155.52�@�� ���@271.08 �� |
�� �� �� |
���@87.6543�@cho�� |
| 87.6543�@cho���@�� | �� �� �� |
�@�Ђ炫
�`�����O���[�h�@�́@���������@����
���[�}�[�@�́@�� �� �V �R �p �x �� �� �l�@���
�u�@�܂��傤�߂�@( �����Ђ傤 )�@����@�́@�ځ@�Ђ炫�@�v�@
���@���Ƃ߂��܂��B
�@�ځ@�Ђ炫�@�@���@�@�R�@���Y �l�@�@�~�@�@�P�W��
�ꂢ�F�@54.735 ��
�Ђ���@�܂��@�ȂȂ߁@����
�S���@�ځ@�����@�n�}�@��@�i�V�S���� �@
38.07450080607�@cho���@���@
���������@�����@���@���イ����@���܂�
38.07450080607
3.040867
������@�P�W�@���@(�@���Y�@�Ɓ@�ǂ����@�́@�ւ����@)�@���܂�
3.040867�@�~�@18�@���@54.735606
54.735�@��
�S���@�ځ@���������ā@�i�~�R�@�ǂȂ��@
����ۂ������@�́@���ǁ@�́@�݂Ђ炫�@������
�@��������
���傤���@�́@���Ӂ@���@�q���g�@�Ɂ@�����Ă݂܂����B
�u�@�R, �Z�@���@(�@����낭�Ӂ@)�@�v..�@�� �悤��
����Ł@
�R�}�@�́@�����@���@���傤����@�́@�ǂ��ɂ��邩�@���@�킩��܂�
�@�@�������@�@�@�@�@�������������@
�Ђ���Ɂ@�R�}�X�@�����Ɂ@�U�}�X�@�́@����@�Ɂ@���@���@���邱�Ɓ@���@���߂��Ă��܂�
���Ӂ@�́@�}�X �߁@���@�ǂ��ɂ��@���ā@����������@�Ł@���߂��Ȃ����@�����Ă݂܂���..
�@�@�ǂ����@�X�^�[�g�@( ���� )�@�́@�}�X�@���@���߂� �A
�@�@�@��������@������Ɂ@
�@�@�@�P �� �Q �� �R �� �c�ƁA�������Ă䂫�@ �c�� �X�}�X �߁A( �͂� ) �܂Ł@������
�@�@�@���́@���傤�@�Ɂ@������
�@�@�@�P�O �� �P�P �� �P�Q �� �c�@�Ɓ@
�@�@�@���� �Â��@���@�������Ă������Ƃɂ��Ă͂ǂ����H�@�Ƃ����Ă݂܂���
�������A
�@�@�@�����@�́@��肩�����Ɓ@�P�@���傤�@�����ށ@���тɁ@�����@�P�P�^�@��
�@�@�@�P �}�X ���@�Y�� �Ă��܂��܂�
�����@���傤����@���@�X�~�X�@�}�X�ł͂Ȃ��@
�@�@�@�P�O �~ �P�O�@�}�X�@�������@�Ȃ�@�ǂ��Ȃ邩�H�@�Ɓ@�ӂ���܂��Ă݂܂���
�@�@�@
����Ɂ@�����@���傤����@���@�P�O �~ �P�O�@�}�X�@�������@�Ƃ�����
�@�@�@�@���Ƃ��@�u �R,�Z �� �v..�@���@
�@�@�@�@���̂܂܁@�u �O�\�Z�@��߁@�́@�}�X�@�Ɂ@ �� �v
�@�@�@�@�Ɓ@����������Ă��@�Ɂ@�C���[�W�@���₷���Ȃ�܂�
�����Ł@�����
�@�@�@�����@���傤����@���@�ւ�@�́@�����݁@�́@�䂩�@�Ɂ@��������@�P�O�O�@���傭�߂�@
�@�@�@�����߂��Ă�����@�ǂ��Ȃ邩�H�@�Ɓ@�Â��Ă݂܂���
�@�@�@�P�O�O�@���傭�߂�@�Ɓ@�����̂�
�@�@�@���R�@�P�O�@���傭�߂�@�~�@�^�e�@�P�O�@���傭�߂�@�́@
�@�@�@�����ق������@�́@�͂����@�ŁA�@���́@�������@�Ȃ�
�@�@�@���傭�߂�@���@�Ȃ���́@���@
�@�@�@�}�X�@�́@���@�Ɓ@���Ȃ��@�悤��傤�Ł@���Ă����܂�
�@�@�@�@�@���イ����@�Ɂ@���Ƃ���Ȃ�
�@�@�@�@�@�Ƃǂ��ӂ���@���@���@���@���傤���@���@���@��
�@�@�@�@�@�́@�悤�ȁ@�C���[�W�@�Ł@�����Ă����܂�
�@�@�@�@�@���R�@�S�@��߂́@�^�e�@�Z�@��߁@�Ɂ@����@���傤����@��
�@�@�@�@�@���R�@�R�@��߂́@�^�e�@�Z�@��߁@�́@�}�X�@�Ɂ@�@
�@�@�@�@�@�u �� �v�@���@����Ȃ�
�@�@�@�@�@�@�S�U�R�U ��
�@�@�@�@�@�@������҂Ⴍ���イ�낭�@�u�Ӂv
�@�@�@�@�@�@�Ł@���������@���@�ł���@�Ɓ@�����Ă݂܂���..
�����
�P�O����ق��@�́@���������@�Ɓ@�������傤���@�����@�Ɓ@�����Ă݂܂����B
information���m�点
-
�x�f���̂��m�点
���������́A�w��̂��߁A�x�f���܂��B -
��������������
���N�`���̊m�ۂ��ł��܂����B��@��t�A�܂��͓d�b�ł��₢���킹���������B -
���N�ی��ɂ���
��f�̍ۂ́A�K�����N�ی������������������B
�ی����Ȃ��ꍇ�A����ł̐f�ÂɂȂ�܂��̂ł����ӂ��������B
Render view�_(^��^)�^
��1v3-0vv0
��v�s�����恛����1-v-3
TEL yone12053.zouri.ne.jp
FAX 03-1vv4-0001
�@�@�@�� �����N�S
�@�@�@�� �����N�R
�@�@�@�� �����N�Q
�@�@�@�� �����N�P
�@�@�@�� ���ǂ�