8くわっど に ついて ..
4くわっど へんしゅうちゅう じげん ( 3じげん+ )
| 【 じげん ( 3じげん + ) 】 ぶんや によって ことば の つかわれかたに かなり ちがいが あります。たとえば 【 きこうがく 】では ロボット の かんせつ の かず に つかわれたり、【 ぶつり 】では なにかしら の たんい と セット で りょう の しゅるい や エネルギー の せいしつ の くぶん に つかわれます。また 【 にちじょう かいわ 】 では べつ の みかた。べつのものさし。たんい。ケタ。きぼ。レベル。など の ような いみあいで したしまれています。 ほん サイト では 【 すうがく 】 における 【 じげん 】 を かんがえていきます。【 ぶつり 】 では 4じげんめ に じかんじく を おいた 【 じくう 】 という かんがえ が ありますが、この サイト で あつかう【 すうがく 】 の じげん では 4じげんめ は じかんじく ( を おくこともできますが、きほんてきに じくう の 意 図 ) では あつかいません。4ほんめ の 【 じくほうこう 】 として、2ほんめ や 3ほんめ の じく と まったく おなじ あつかい で みていきます。 この ページ は みどり いろ なので、おもに、【 かんれんようご 】の ことば の イミ や いっぱんてき な さんこう じょうほう ( しらべて えられる ちしき ) 。について とりあつかっていきます。 |
  |
ページ ないに げんざい ある こうもく ( へんしゅうちゅう )
■ +と− の ふたほうこう ■ マイナス ほうこう ■ 【 かんれんようご 】
■ スリーディー ■ すうがく の 4じげん ■ ぶつり の 4じげん ■ しゃこう ざひょう
■ こさいん90ど の ふごう ■ ぜろ じょう ■ かつさんかくかんすう
■ かつさんかくかんすう の シグナル ■ ながさ の るいじょう ■ ながさ の むじげん
SIGN しぐなる かんすう
+1 か −1 ( か0かの 符 号 ) にします
かけざん や わりざん と くみあわせることで
ふごう の ちょうせい が できます
ふごう を かえたくないときは +1 を かけます ( ± そのまま )
ふごう を かえたい ときは −1 を かけます ( ± ぎゃくふごう )
第 三 角 法 による 『 4 quad 』
だいさんかくほうないよう 1 2 3 4 5 6 7 8
ナビゲーション
. |
『 quad 』 の かんれん わーど |
| 後日どこか(の頁)に配置予定 参考関連単語 クワッド ユークリッド 空 間 直 交 座 標 系 象 限 (直 交 と↓斜 交 これとは、ちがいます) 斜 交 座 標 系 |
◆ きにゅう の じゅんばん ( ,カンマ で くぎる xyz ( 2,3,4 ) ) ◆ ひりつ が おなじなら そうじ
SIGN しぐなる かんすう+1 か −1 ( か0かの 符 号 ) にします かけざん や わり 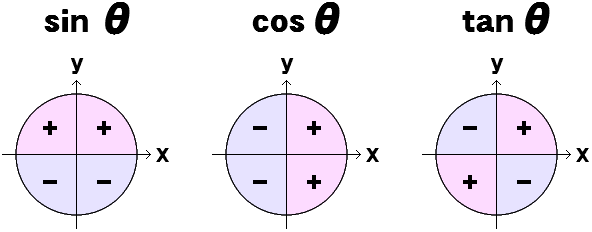 SIN は うえ + COS は みぎ + TAN は たすきがけ + ぎゃくすう に ついて も おなじ ( メモ ) |
|||||
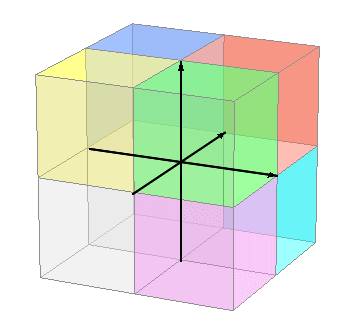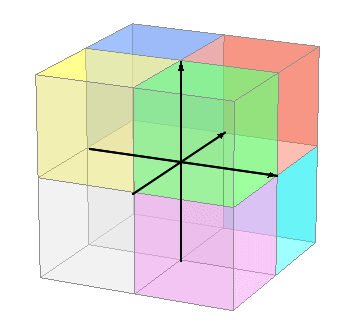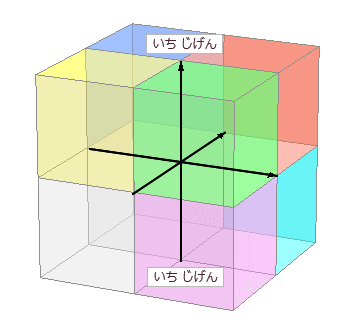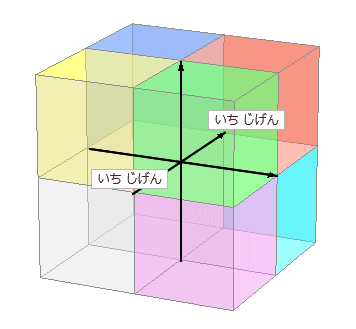 |
【 超 重 要 】 ひとつ の じげん ( それぞれ の じげん ) には + と − の ふたほうこう が あります。 どちらか かたほう を さだめた しゅんかん に もう かたほう の ( ぎゃく の ) ほうこう は 「 〜 の マイナス ほうこう 」 と じどうてき に よばれることに なります。 → 思 : イメージ |
||||
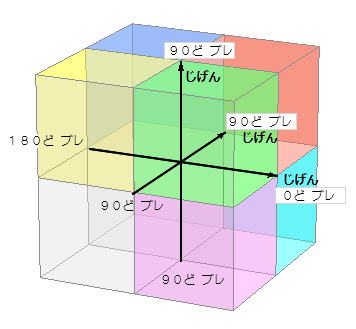 |
( それぞれ の じげん の ) マイナス ほうこう それぞれ の じげん にとっての マイナス ほうこう は もと の プラス ほうこう の ぎゃく ほうこう に なります。 この ぎゃく ほうこう という のを 「 かいてん 」 で いうなら 「 はんしゅう 」 した ほうこう に なります。 「 カクド 」 で いうなら 「 ひゃくはちじゅう ど 」 に なります。 この カクド を べつの たんい で ひょうげん すると こうなります。
に なります わかること ( → 2じげん・3じげん の 値 ) |
||||
 |
【 くわっど 】 の かんれん ようご 長 文《 中 略 》 m(_ _)m ↓ るいじょう 後日追加 仮予定 ( べきじょうは→虚数4で仮) かんれんようご について の さんこう 象 限 しょううげん quadrant くわっど 直 交 座 標 系 ちょっこう ざひょうけい ユークリッド 空 間 ゆうくりっど くうかん ( → かみくだく 思 ) |
||||
   |
スリーディー は さんじげん 3D の 「 D 」 に ついて 【 Dimension 】 ( ディメンション )次元 。 に なります。 【 3D 】 ( スリーディー )で 三次元( おおくのばあい 立体 ) を いみします。 みっつ の じげん で スリーディー。 3D。 当 サイト では 当サイト では ほとんどの こうもく で 2D を へいめん として とらえて 3D を くうかん として とらえています。 そのさい、 2D は たかさの ない せかい。 3D は たかさの ある せかい として とらえています。 AI デジタル かくにん → 分 |
||||
 |
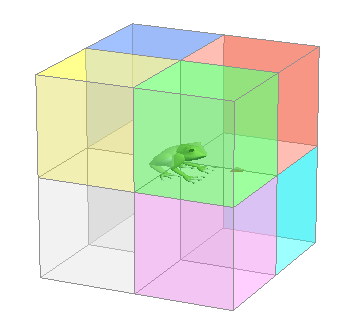
【 超 重 要 】 すうがく の 4じげん 【 4D 】 でぃー dimension ディメンション じげん よっつ の じげん で フォーディー ( フォーディー )。 三次元 に あらたに 直 交 する じく を もう 1 本 ついかします。 └ おもうこと イメージ └ かんがえたこと なまえ このついかされる じく は ( きほんてき に ) じかんじく ではありません。 ( └ じかんじく に することもできますが、) すでにある 6ほうこう( 3じげん じくの それぞれの プラスマイナス 2 ほうこう ) の どの ほうこうとも ちょっかく に ぶつかっ( 直 交 し )て はなれていく という 架 空 の ほうこう の ひろがり を かくちょうして せってい してみた くうかん の せかい。 すうがく 次元 点の位置は,線上では一つ,面上では二つ,空間内では三つの実数(座標)で表され,この意味で線・面・空間をそれぞれ1次元空間・2次元空間・3次元空間であるという。これを拡張して4次元,n次元,無限次元の空間が考えられる。またベクトル空間では,一次独立なn個のベクトルの組が存在し,n+1個以上のベクトルの組はすべて一次従属であれば,次元はnであるという(ベクトル空間)。次元の概念はさらに距離空間や位相空間にも導入され,より厳密な定義を与えられている。 当 サイト では すうがく の 【 4 じげん 】 を あつかいます。 AI デジタル かくにん → 分 思 : おもうこと はなれぐあい ・ 4Dえいが SFえいが …時空 サーモグラフィー は 4じげん ビジョン(と、おもう) エネルギー の しゅるい の イメージ 熱 重 電 音 香 金.. ほか多数 考 : かんがえたこと もげ ・ ちょもあーくふぉーでぃー ざひょうじく( や ながさ・キョリ の ような ) いわゆる 「 はなれぐあい 」 として とらえていくと イメージ しやすくなります。−−おもうこと ↓ えいがかん の 4D びじょん は +振動など特殊体感エフェクトじげん |
||||
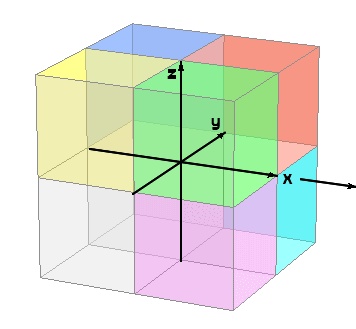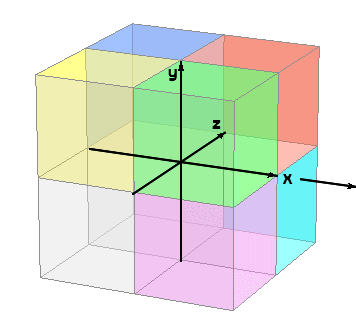 |
【 超 重 要 】 ↓ ぶつり の 4じげん と ↑ すうがく の 4じげん は べつもの でぃー dimension ディメンション じげん よっつ の じげん で フォーディー ぶつり 次元 ディメンションとも。ある物理量が長さL,時間T,質量Mなどの基本的な物理量とどのように関係するかを示す構造。たとえば加速度Aは[A]=[LT(-/)2]の関係をもち,長さにつき1次元,時間につき−2次元である。 ひかり の はやさ 2.99792458×108m/sec。 びょうそく 30 まん キロ。 1 びょうで ちきゅう 7しゅうはん。 当 サイト では ぶつり の 【 4 じげん (じくう)】 は あつかって いません。 m(_ _)m AI に しつもん してみる → 分 |
||||
 ちょっかく ⊥ で マスメ が くまれています |
90ど で まじわっていない ( 直 交 「 ちょっこう 」では ない ) 90ど で まじわっていない 座 標 系 も あるようです さんこう → こちら ( ななめ に まじわる と かいて 斜 交 「 しゃこう 」 というものも あるようです。 ほん サイト であつかうもの は これとは、ちがいます ) ほん サイト は 直 交 座 標 系 のみ を あつかうので 斜 交 座 標 系 は べつもの に なります。 ( ねんの ため の ことわり に なります。) |
||||
 さかいめ の ふごう は プラス でも マイナス でも ない  |
【 こさいん 90 ど 】 の ふごう こさいん 90ど の ふごう は …
90 ど は すいちょく ⊥ で まうえ ↑ なので、 みぎ ブレ も ひだり ブレ も ありません。 つまり +プラス にも −マイナス にも ぞくしません。 イコール ぜろ。(0)。に なります。 → こちら 分 (クリック) では それが うまく いきません。 「 正 」 の かず。と でてしまいます。 → たいさく 考 どうように ぎゃくかいてん や いっぱんかく でも 0 に なります。 ( 0 に ならなくては いけません )
|
||||
 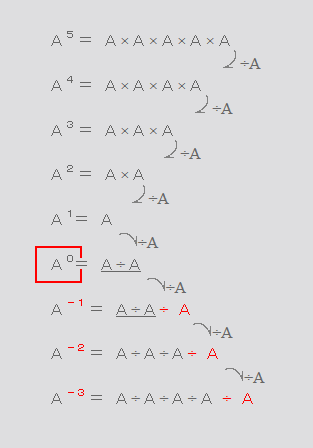  |
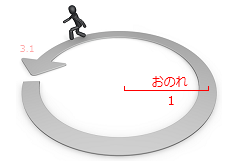
ちょうせいちゅう ぜろ じょう の しょうたい A0 に ついて えー の ぜろじょう は = 1 に なります。  ひだり の しき を みてみます。 いちだん あがる ごと に ×( おのれ ) が かけられています。 これを ぎゃく に かんがえると いちだん さがる ごとに ÷( おのれ ) で わられてもいます … そう とらえると 1 じょう や 0 じょう も あつかえるように なっていきます。 つまり ぜろ じょう とは ... かんたんに いうと 、 「 おのれ ÷ おのれ 」 に なります。 これを ぶんしょう もんだい ふうに かきかえると .. おのれ の なかに おのれ が なんこぶん ありますか ? となり その こたえは 「 = 1 こ 」 と なります。 しみゅれーしょん → 分 かんがえたこと → 考 おもうこと → 思 |
||||
  |
【 ぎゃくすう 】 A の ぎゃくすう は 「 1 ÷ A 」 に なります。 いいかたを かえると A ぶん の いち とも いえます。 さんかく かんすう の ぎゃくすう も さんかくかんすう ぶん の いち に なります。 1 ――――――――――― さんかく かんすう さいん の ぎゃくすう = こせかんと こさいん の ぎゃくすう = せかんと たんじぇんと の ぎゃくすう = こたんじぇんと 1 ÷ さいん θ = こせかんと θ 1 ÷ こさいん θ = せかんと θ 1 ÷ たんじぇんと θ = こたんじぇんと θ 1 ――――――― = CSC θ SIN θ 1 ――――――― = SEC θ COS θ 1 ――――――― = COT θ TAN θ こせかんと 、 せかんと 、 こたんじぇんと これら 3つ を 【 かつ さんかく かんすう 】 割 三 角 関 数 といいます。 分: わかること 「 ÷ たんじぇんと 」 ←は→ 「 × こたんじぇんと 」 思: おもうこと ムリスウでわるって、?→ ひとまず デンタク さま |
||||
| ↑ カンスウ の 4 クワッド の ↓ 【 しぐなる ( ふごう ) 】 かつ さんかくかんすう の シグナル ( ± ふごう ) は ぎゃくすう に するまえと おなじ に なります  さいん こさいん たんじぇんと ぎゃくすう に すると おおきい ⇔ ちいさい は ぎゃくてん しますが、 ふごう ± は ぎゃくてん しません ↓ 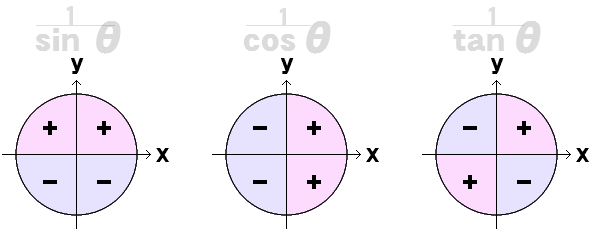 ↑ この 2ばんめ と つぎの ↓ 3ばんめ は まったく おなじ いみ に なります 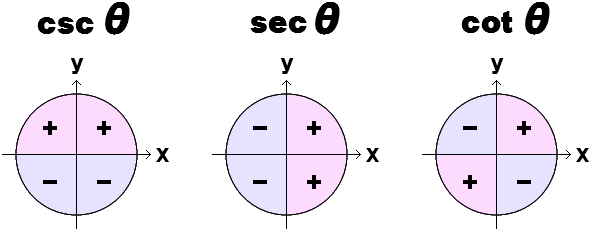 こせかんと せかんと こたんじぇんと たて 3だん を みくらべると ± ふごう の いちかんけい は かわっていません 思 : ぎゃくすう → てこ の げんり |
|||||
 |
【 ながさ 】 から できる じげんりょう たいせき は ながさ の さん じげんりょう めんせき は ながさ の に じげんりょう ながさ は ながさ の いち じげんりょう |
||||
  |
∠ かくど は 【 ながさ 】 の む じげんりょう ( ∠ ラジアン について デジタル かくにん 1 2 3 ) たいせき は ながさ × ながさ × ながさ めんせき は ながさ × ながさ ながさ は ながさ かくど は ながさ ÷ ながさ しみゅれーしょん → 分 かんがえたこと 「 1 cm 0 」 が あるとしら → 考 |
||||
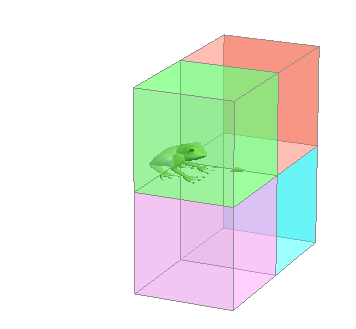 |
こちら が まえ 4くわっど に なります。 ■■■■ すくなくとも 2 パイステラジアン の はんい に なります おおきくとも ∠ みひらき が 90ど いない に かならず なります |
||||
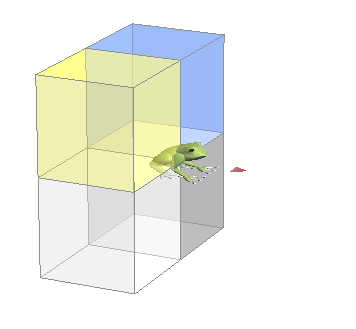 |
こちら が うしろ 4くわっど に なります。 ■■■■ すくなくとも うしろ に すすんで いる ことに なります すくなくとも ∠ みひらき が 90ど いじょう に かならず なります |
||||
( 編集中 ) −−−−つづき−未ラベル リンク−−−− えすあいたんい SI 単 位 メモ整理中 仮自分用リンク ロンエネ おもうこと → やわらかく かくちょう 人・冊・個・円 助数詞 → 単位 として |
|||||
| |
|||||
もどる
( 知 思 分 信 考 )
サイト ない ていぎ この ページ の ないよう は しんじている こと というよりも、↓ サイト ない ていぎ ( ゼンテイ で もちいる ことば の やくそく ) に なります。 ■ もどる |
■ もどる  |
copyright©2022 Render view all rights reserved.