8くわっど に ついて ..
4くわっど へんしゅうちゅう じげん ( 3じげん+ )
| 【 じげん ( 3じげん + ) 】 ぶんや によって ことば の つかわれかたに かなり ちがいが あります。たとえば 【 きこうがく 】では ロボット の かんせつ の かず に つかわれたり、【 ぶつり 】では なにかしら の たんい と セット で りょう の しゅるい や エネルギー の せいしつ の くぶん に つかわれます。また 【 にちじょう かいわ 】 では べつ の みかた。べつのものさし。たんい。ケタ。きぼ。レベル。など の ような いみあいで したしまれています。 ほん サイト では 【 すうがく 】 における 【 じげん 】 を かんがえていきます。【 ぶつり 】 では 4じげんめ に じかんじく を おいた 【 じくう 】 という かんがえ が ありますが、この サイト で あつかう【 すうがく 】 の じげん では 4じげんめ は じかんじく ( を おくこともできますが、きほんてきに じくう の 意 図 ) では あつかいません。4ほんめ の 【 じくほうこう 】 として、2ほんめ や 3ほんめ の じく と まったく おなじ あつかい で みていきます。 この ページ は あお いろ なので、おもに、シミュレーション に よる ぐたいてきな データ ( さんこうけっか・サンプル ) を あつめます。そこから みえてくる ケツロン ( きょうつうてん ) を さがしていきます。 |
  |
ページ ないに げんざい ある こうもく ( へんしゅうちゅう )
■ 1D の カクド ■ 3ほんじく3D(要編集) ■ 未
■ 2Dも3Dも 0なら(要編集) ■ 2Dも3Dも 0なら (2)(要編集)
■ 1Dが0なら(要移動xyz) ■ 1Dがほぼ0なら(要移動xyz)
■ 1Dが負なら(要移動xyz) ■ ケタ がえOK(3D例要) ■ 180ど を こすと
■ さいだい 180ど ■ マイナスカクド が おなじ
■ ぶつり4D と すうがく4D ■ シグナル かんすう サンプル(要編集)
■ かけざん/わりざん1 ■ かけざん/わりざん2
■ かけざん/わりざん3 ■ ぎゃくすうれい ■ よくめにする しょうすう
■ コサイン90ど の ふごう ■ X が 正 なら(要移動xyz) ■ X が 負 なら(要移動xyz)
■ ゼロ じょう ぐたいれい
■ 未 ■ 未 ■ 未
ナビゲーション
. |
『 quad 』 の かんれん わーど |
◆ じくのかくど は 90ど の ばいすう(180、270)
click   |
いち じげん なら ∠ 0 ど か ∠ 180 ど ( こちら : → 思 では ∠ カクド が ない。 と あります ) が、 げんみつには はかってみれば、∠ カクド は あります。 げんてん よりも すすんで いるなら → ∠ 0 ど もどって いるなら → ∠ 180 ど に なります。 |
||||||||||||||||||||
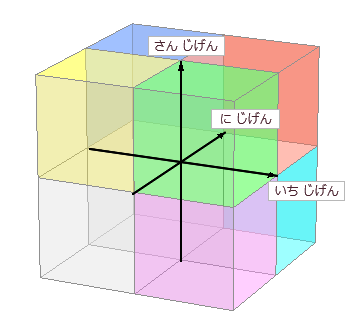 |
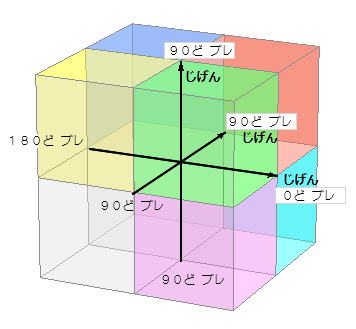
じく が 3本 だから スリーディー y と z の どちら を たかさ や おくゆき に するか は それぞれ の つごう に あわせて じゅうなん に おきかえて ください ( → みぎて 系 ソフト ひだりて 系 ソフト ) 【 重 要 】jigen xyz いずれも 、90ど で こうさ ( ちょっこう ⊥ ) している という こと が きょうつうてん に なります G:cos90deg=0% kyobu R:mouten jigen --xyz -3D |
||||||||||||||||||||
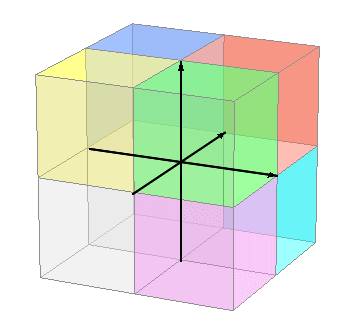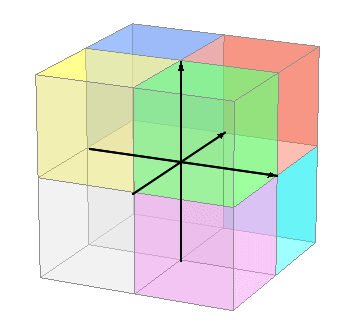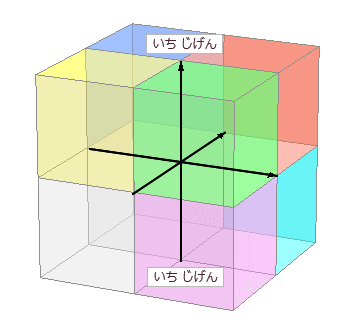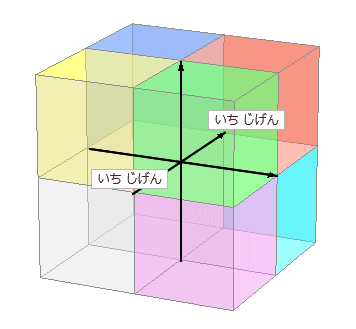 |
じく が 3本 だから スリーディー y と x じく ライン は この ほうこうが きじゅん( ∠ みひらき 0ど )に なります これは ちきゅうぎ にえんかく でいうところの ヌルとう に なります |
||||||||||||||||||||
 |
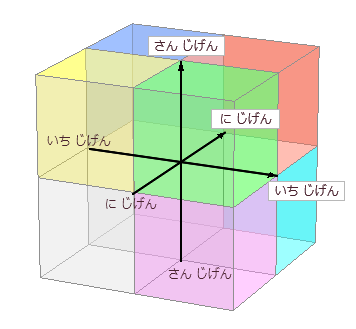
「 いちげん の ライン 」 は 0 ど こちら の ていぎ に より ( → 信 ) いちじげん じく の プラス の ほうこう は くうかん かくど 「 0 ど 」 ほうこう に なります。 かみくだくと、 に じげんめ と さん じげんめ の あたい が ない なら、 ( に じげんめ と さん じげんめ の あたい が ゼロ なら、) 「 0 ど 」 ほうこう に なります。 ※ ↑ または こちら も ありえます ↓ ※ |
||||||||||||||||||||
 |
「 いちじげん の マイナス ライン 」 は 180 ど こちら の ていぎ に より ( → 信 ) いちじげん じく の マイナス の ほうこう は くうかん かくど 「 180 ど 」 ほうこう に なります。 いいかた を かえると、 ほか の じげん の あたい が ない なら、 ( ほか の じげん の あたい が ゼロ なら、) 「 0 ど 」 か 「 180ど 」 ほうこう になります。 知 ( → ぎゃくほうこう の べつ の ひょうげん ) |
||||||||||||||||||||
| |
|||||||||||||||||||||
  |
「 いちじげんめ が ぜろ 」 なら ⊥ 90 ど こちら の ていぎ に より ( → 信 ) えっくす の あたい が プラス でもなく、 .. マイナス でもなく、 ぜろ 、 ( で Y か Z に わずか でも ± あたい が あれば ) くうかん かくど は 「 ⊥ 90 ど 」 の ひらき になります。 れい XYZ ( ぜろ , -2 , -1 ) XYZ ( ぜろ , 4 , -777 ) XYZ ( ぜろ , 500 , 0 ) これら ↑ は YZ へいめんじょう の いち なので、いずれも 「 ⊥ 90 ど 」 の ひらき になります |
||||||||||||||||||||
 |
X が ぴったり ぜろ では ないにしても … 「 X が ほぼ ぜろ 」 なら ほぼ ⊥ 90 ど X が ぴったり ぜろ では ないにしても … 0.0001 や 0.00002 など の ように、 ほか の Y , Z 値 とくらべて 2 ケタ くらい ちがうような .. あっとうてき に ちいさいとき は けっかてき に くうかん かくど は 「 ほぼ ⊥ 90 ど 」 の ひらき になります。 れい x y z( -0.01 , -2 , -1 ) ∠ 90.3 ど x y z( 0.002 , 4 , -777 ) ∠ 89.9 ど x y z( -0.0003 , 500 , 0 ) ∠ 90.00003 ど x y z( 0.00004 , 500 , -777 ) ∠ 89.99999 ど 未 メモ思うこと→ カニ そよ風が ふいてる おいかぜ+ むかいかぜー 後日1227 |
||||||||||||||||||||
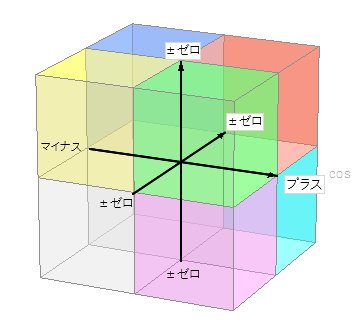 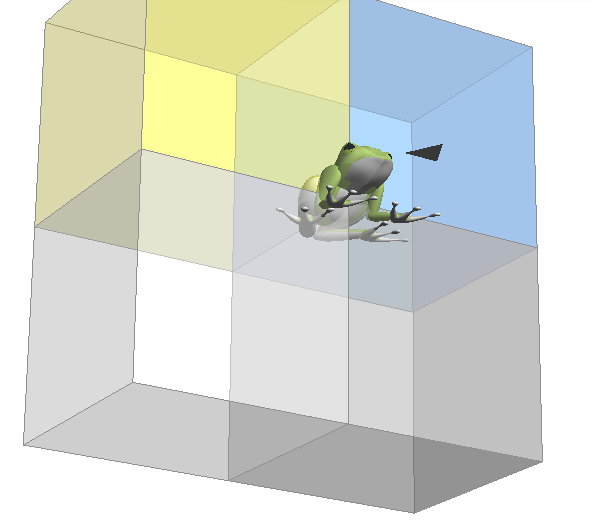 |
x が 「 まいなす 」なら かならず 90 ど いじょう れい
x が 「 まいなす 」 なら かならず 90 ど いじょう に なります。 まよこ ( や まうえ ) が 90ど に なり それよりも うしろ の ブロック の エリア なら それる カクド が 90ど よりも おおきく なります。 カクド 値 は おおよそ に なります。 ( ぴったりでは ありません ) |
||||||||||||||||||||
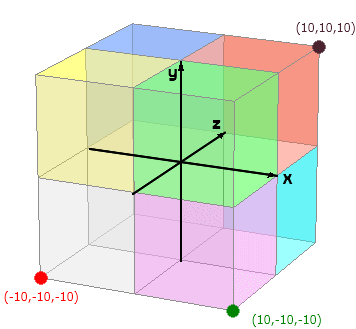 1 マス 10 めもり |
( ながさ の ) ケタ が かわっても カクド は かわりません ぜんたい てき に 10 ばい サイズ に なっても ひりつ が おなじ なので ∠カクド は かわりません。 x y ( 2 , 2 ) の かくど は ∠ 45 ど x y ( 20 , 20 ) の かくど も ∠ 45 ど x y ( 200 , 200 ) の かくど も ∠ 45 ど x y ( 2 まん , 2 まん ) の かくど も ∠ 45 ど x y ( 2 おく , 2 おく ) の かくど も ∠ 45 ど x y ( 0.002 , 0.002 ) の かくど も ∠ 45 ど かくだいコピー しゅくしょうコピー の ような かんじに なります ( そうじ ずけい ) 3じげん ( xyz ) でも これは かわりません。 |
||||||||||||||||||||
  |
∠ 180 ど いじょう それて いくと .. かくど に おいて さいだい の ひらき は つうじょう ∠ 180 ど (= はんしゅう ・1ぱい ) に なります。 では、 ∠ 181 ど など 、それを こすと どうなるか というと … むしろ ∠ ピント が あいはじめ ていきます … ∠ 181 ど は 、ぎゃく かいてん にて ∠ 179 ど の ひらき と なります。 ∠ 360 ど − ∠ 181 ど = ∠ 179 ど おなじように もし ∠ 350ど なら、ぎゃく かいてん にて ∠ 10 ど の ひらき と なります。 ∠ 300ど なら、ぎゃく かいてん にて ∠ 60 ど の ひらき と なります。 へんしゅうちゅう |
||||||||||||||||||||
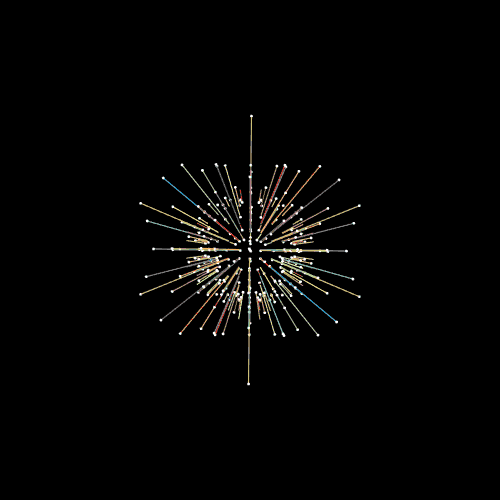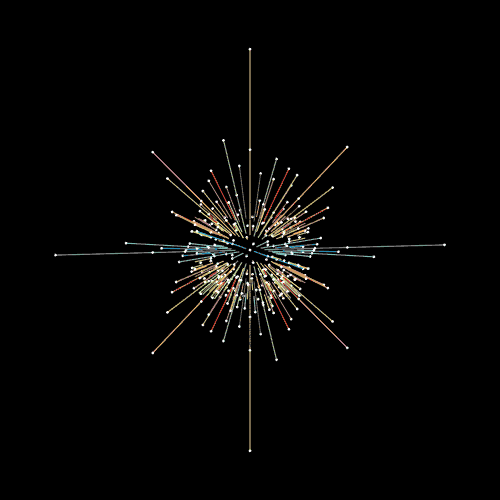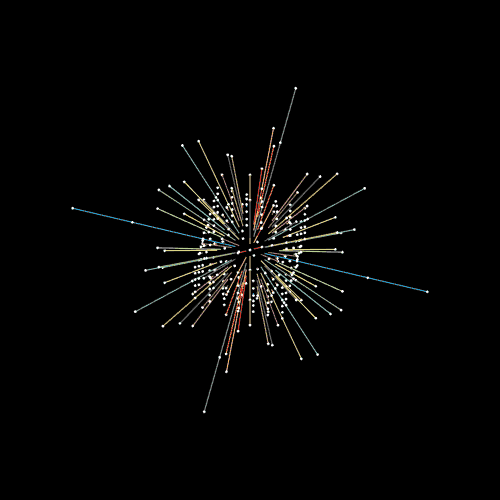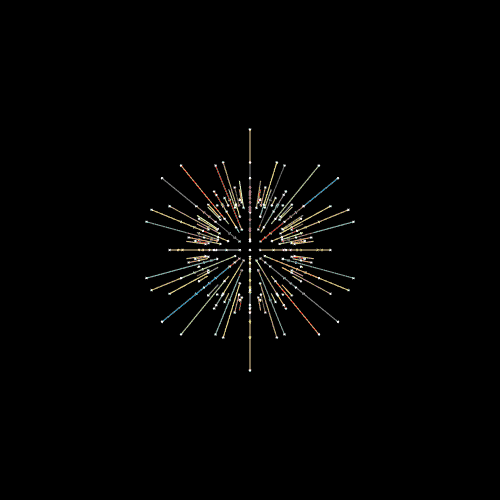 |
( ∠ かいてんりょう としてとらえずに ) ∠ ひらき ( ブレ ) だけでいうと、 ∠ 180 ど が MAX ∠ 180 ど いじょう ∠ そらそう としても そらせません。 ∠ 180 ど いじょう ∠ ブレ る ことはありません。 なぜかというと、 ∠ 180 ど が 「 マイナス えっくす じく 」 の ほうこう だから に なります。 |
||||||||||||||||||||
マイナス かいてん でも おなじ カクド ∠180 ど ちてん と ∠マイナス 180 ど ちてん は おなじ ∠ 0 ど ちてん と ∠マイナス 0 ど ちてん は おなじ ∠360 ど ちてん と ∠マイナス 360 ど ちてん は おなじ |
|||||||||||||||||||||
| コンピューター AI に 「 4じげん 」 について たずねてみました。 「 物理 の 4次元 時空 」 と 「 数学 の 4本目 の 直交 する 軸 の 4次元 」 の ちがい について |
|||||||||||||||||||||
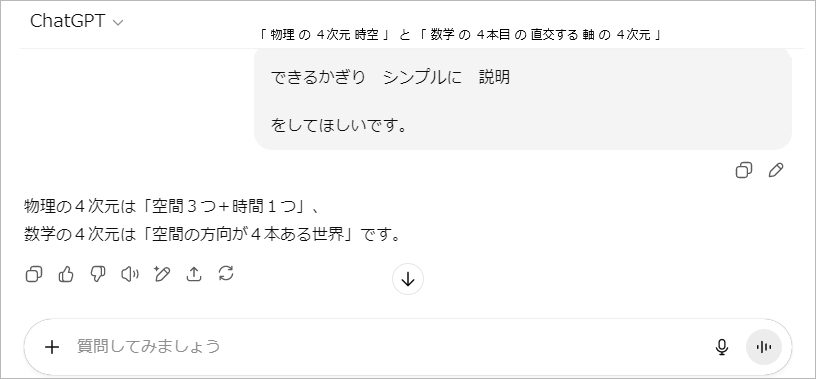 AI かくにん でも 「 知 : こちら 」 と おなじこと を いっていることが わかります。 |
|||||||||||||||||||||
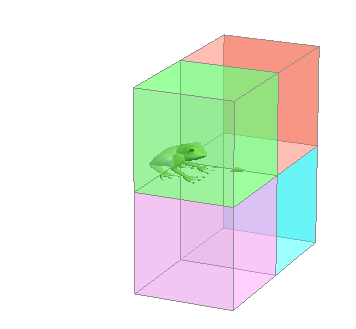 |
( G: SIGN しぐなる かんすう ) の ぐたいれい 6〜10こ ぜんご |
||||||||||||||||||||
 |
ミラー は おなじ |
||||||||||||||||||||
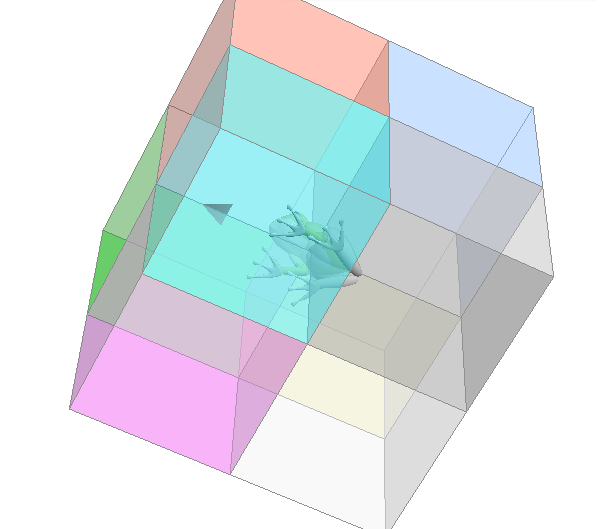  |
( かける ⇔ わる ) × たんじぇんと は ÷ こたんじぇんと 2 × tan 30 ど = 2 ÷ cot 30 ど = 1.154.. 3 × tan 30 ど = 3 ÷ cot 30 ど = 1.732.. 4 × tan 30 ど = 4 ÷ cot 30 ど = 2.309.. : 百 × tan 30 ど = 百 ÷ cot 30 ど = 57.735.. ÷ たんじぇんと は × こたんじぇんと 2 ÷ tan 30 ど = 2 × cot 30 ど = 3.464.. 3 ÷ tan 30 ど = 3 × cot 30 ど = 5.196.. 4 ÷ tan 30 ど = 4 × cot 30 ど = 6.928.. : 百 ÷ tan 30 ど = 百 × cot 30 ど = 173.20.. → 知: ぎゃくすう 思う → たてよこひ tan よこたてひ cot 未 |
||||||||||||||||||||
  |
( かける ⇔ わる ) × こさいん は ÷ せかんと 2 × cos 30 ど = 2 ÷ sec 30 ど 3 × cos 30 ど = 3 ÷ sec 30 ど 4 × cos 30 ど = 4 ÷ sec 30 ど : 百 × cos 30 ど = 百 ÷ sec 30 ど ÷ こさいん は × せかんと 2 ÷ cos 30 ど = 2 × sec 30 ど 3 ÷ cos 30 ど = 3 × sec 30 ど 4 ÷ cos 30 ど = 4 × sec 30 ど : 百 ÷ cos 30 ど = 百 × sec 30 ど → 知: ぎゃくすう |
||||||||||||||||||||
  |
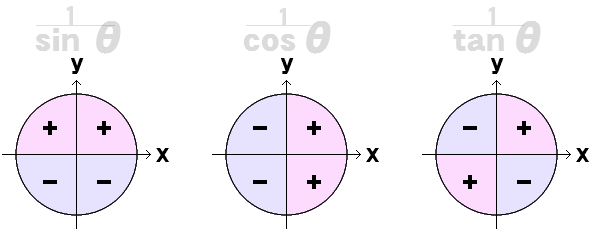
( かける ⇔ わる ) × さいん は ÷ こせかんと 2 × sin 30 ど = 2 ÷ csc 30 ど 3 × sin 30 ど = 3 ÷ csc 30 ど 4 × sin 30 ど = 4 ÷ csc 30 ど : 百 × sin 30 ど = 百 ÷ csc 30 ど ÷ さいん は × こせかんと 2 ÷ sin 30 ど = 2 × csc 30 ど 3 ÷ sin 30 ど = 3 × csc 30 ど 4 ÷ sin 30 ど = 4 × csc 30 ど : 百 ÷ sin 30 ど = 百 × csc 30 ど → 知: ぎゃくすう |
||||||||||||||||||||
| ぎゃくすう しみゅれーしょん 1 の ぎゃくすう は 1 2 の ぎゃくすう は 0.5 3 の ぎゃくすう は 0.333.. 4 の ぎゃくすう は 0.25 5 の ぎゃくすう は 0.2 10 の ぎゃくすう は 0.1 20 の ぎゃくすう は 0.05 100 の ぎゃくすう は 0.01 |
|||||||||||||||||||||
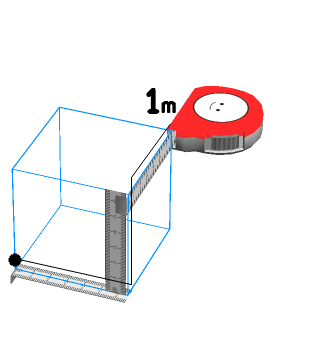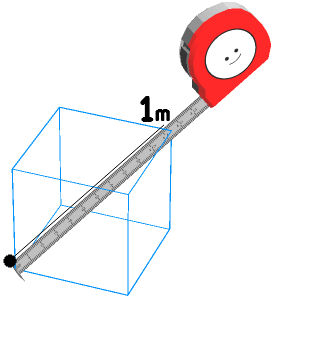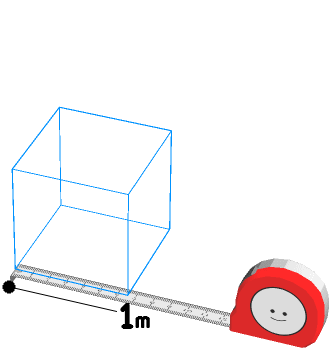 |
ぎゃくすう さんかくかんすう かんれん るーと 1 の ぎゃくすう は 1.00000 るーと 2 の ぎゃくすう は 0.70710 るーと 3 の ぎゃくすう は 0.57735 るーと 0.5 の ぎゃくすう は 1.41421 るーと 0.333 .. の ぎゃくすう は 1.73205 るーと 1.333 .. の ぎゃくすう は 0.86602 さんかくかんすう で よく みかける きんじち に なります。 どこか で これらの すうじを みたら おぼえていると ゆうり に なります。 |
||||||||||||||||||||
 さかいめ の ふごう は プラス でも マイナス でも ない  |
えくせる にて こさいん 90ど の しぐなる は …
ほんらい は このしゅんかんだけ 「 ゼロ 」と でてほしい ところであります。 げんみつ には → こちら 知 くわしくみてみる ために しぐなる を はずしてみます
17 ケタ め ( 10 京 ぶんの1) に わずか に かず が でてきてしまいます。 この えいきょう を うけて しぐなる かんすう を ひっつけると イコール いち。つまり (=プラス1 ) 。と でてしまう ようであります。 → たいさく 考 ためしに 90ど オーバー は 「 負 :( マイナス ) 」で なければなりません すこし ( +0.01 ..など の ように ) だけ かくど を はみださせて みると
→ かみくだく 思 ないよう 1 2 3 4 5 6 7 8 もどる ( 知 思 分 信 考 ) |
||||||||||||||||||||
 |
げんてん と えっくすち を くらべるとき こちら の 4 エリア は 【 ≦ 】 大なり いこーる ( 以 上 ) に なります。 ■■■■ 「 げんてん の えっくすち 」 ≦ 「 あたい の えっくすち 」 えっくすち は げんてん 以 上 に なります すくなくとも したまわる ことは ありません |
||||||||||||||||||||
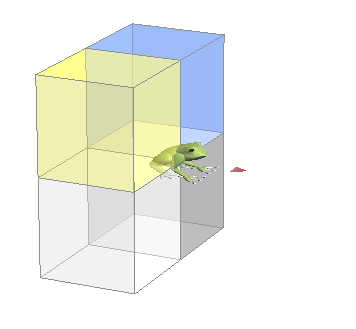 |
げんてん と えっくすち を くらべるとき こちら の 4 エリア は 【 ≧ 】 小なり いこーる ( 以 下 ) に なります。 ■■■■ 「 げんてん の えっくすち 」 ≧ 「 あたい の えっくすち 」 えっくすち は げんてん 以 下 に なります すくなくとも うわまわる ことは ありません |
||||||||||||||||||||
 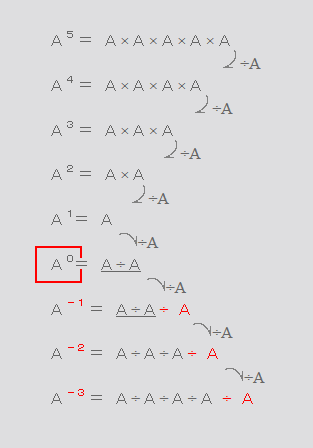 |
ちょうせいちゅう ぜろ じょう の しみゅれーしょん A0 に ついて 
こちら → 知 の じょうほう より たとえば、 3 0 = 3 ÷ 3 になり = 1 と なること が わかります 1 億 0 = 1 億 ÷ 1 億 になり = 1 と なること が わかります しっていること → 知 おもうこと → 思 かんがえたこと → 考 |
||||||||||||||||||||
  |
|||||||||||||||||||||
| |
|||||||||||||||||||||
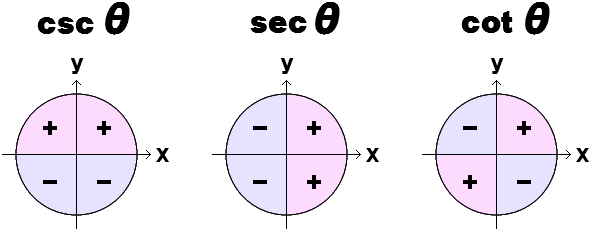
こせかんと せかんと こたんじぇんと
もどる
( 知 思 分 信 考 )
サイト ない ていぎ この ページ の ないよう は しんじている こと というよりも、↓ サイト ない ていぎ ( ゼンテイ で もちいる ことば の やくそく ) に なります。 ■ もどる |
■ もどる  |
copyright©2022 Render view all rights reserved.